GAN #1
Generative Adversarial Nets
Gan利用对抗的方法,提出了生成式模型的新框架。它需要同时训练两个模型(生成模型G和判别模型D),G用于捕获数据的分布,而D需要判别出一个样本是来自训练集还是生成模型。生成模型的目标是尽最大可能让判别模型犯错(无法成功判别数据的来源),G和D在本文中被定义为多层感知机,整个系统通过反向传播来进行训练。
AN analogy to GAN
在生成对抗网络框架中,生成模型与判别互相对抗。可以把生成模型类比为造假币者,判别模型类比为警察。生成模型试图制造假币骗过判别模型,而判别模型努力区分假币。二者在这样的对抗中不断学习提升各自的水平,直到生成模型的造的假币和真的一模一样,判别器无法区分。另外,警察进步不能过大或过小。进步过大时,造假者直接被一锅端,无法继续造假钞;进步过小时,造假者不需进步也能骗过警察,则没有动力进步
Adversarial nets
对抗网络认为数据集代表着一个联合分布,每一个样本都可以由高维随机变量表示。假设数据集是许多张2*2大小的黑白图片,每张图片有四个像素点,于是将该分布看作四维随机变量的分布,每一维代表着一个像素的取值(黑白只取0或1)

在让生成模型学习数据集代表了分布之前,首先定义一个符合高斯分布的先验噪声Z,生成模型就是要学习把Z映射成为数据集代表的分布,MLP理论上可以拟合这样一个函数来完成目标。生成器以Z为输入,输出一个尽量符合数据集分布的样本
判别器也是一个MLP,判别器以数据集或生成器生产的样本为输入,输出一个标量(0:生成器生成的样本,1:真实样本,判别器的输出介于[0,1]),判别样本的真伪。判别器要学习一个二分类任务
D与G对于同一个目标函数采取相反的优化方式:

在不同分布里采样计算后得到期望和,生成器和鉴别器分别要调整参数最大化和最小化这一期望和,体现了对抗的过程,D尽量区分生成的数据和真实数据,G尽量使得生成的数据和真实数据难以区分下图展示了对抗网络训练过程中,各个成分的变化:
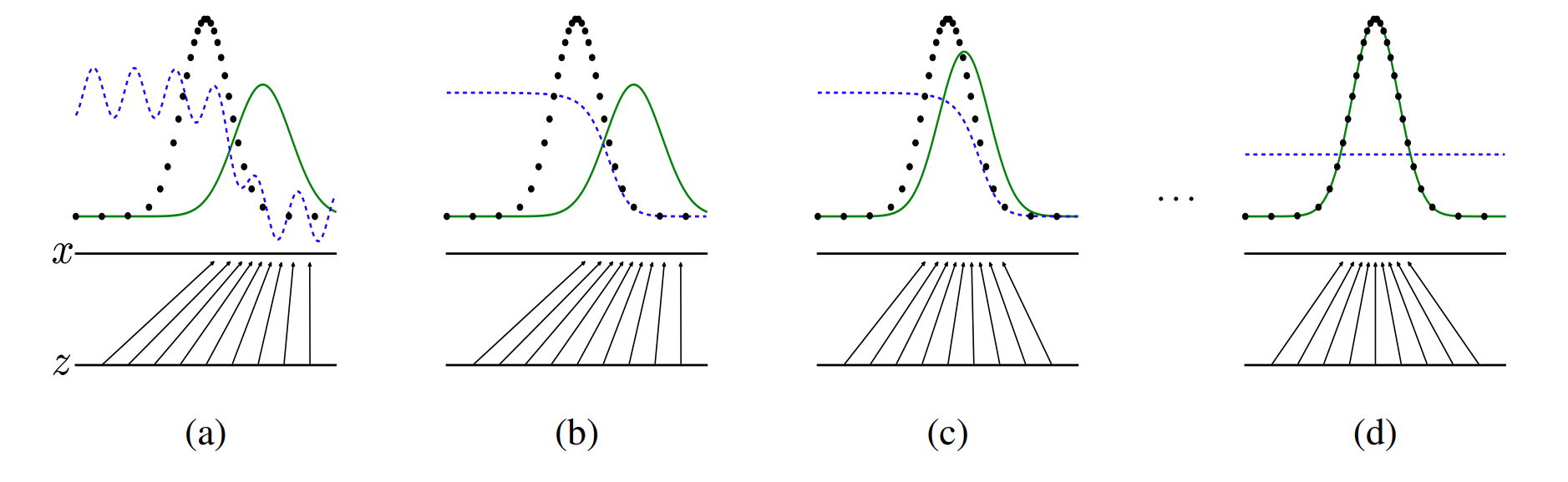
Z为高斯噪声,绿色线代表G生成数据的概率密度函数,黑色线代表真实数据的概率密度函数,蓝色代表D输出标量的函数
(a)G将Z随即映射为另一个分布,与真实分布存在一定差距,此时D未经学习,分类能力弱
(b)固定G,训练D,D分类能力明显上升
(c)固定D,训练G,G学习到把Z向真实数据分布映射
(d)反复多轮后,G映射的分布与真实数据相同,判别器无法区分对抗网络算法流程如下:

先更新D,再更新G,G只与目标函数中后半段有关。k是一个超参数,不能太大也不能大小。取太大判别器训练得太好,取太小判别器变化太小
Theoretical results
- 理论上,对抗网络存在全局最优解:生成器映射的分布等于真实数据分布
- 对抗网络算法可以求解目标函数