ResNet

Residual Network

深层的神经网络通常很难进行训练，本文使用了一个残差学习网络结构来训练比以往的神经网络要深得多的模型。残差网络容易训练，并且在深层神经网络中表现出来较好的准确率。

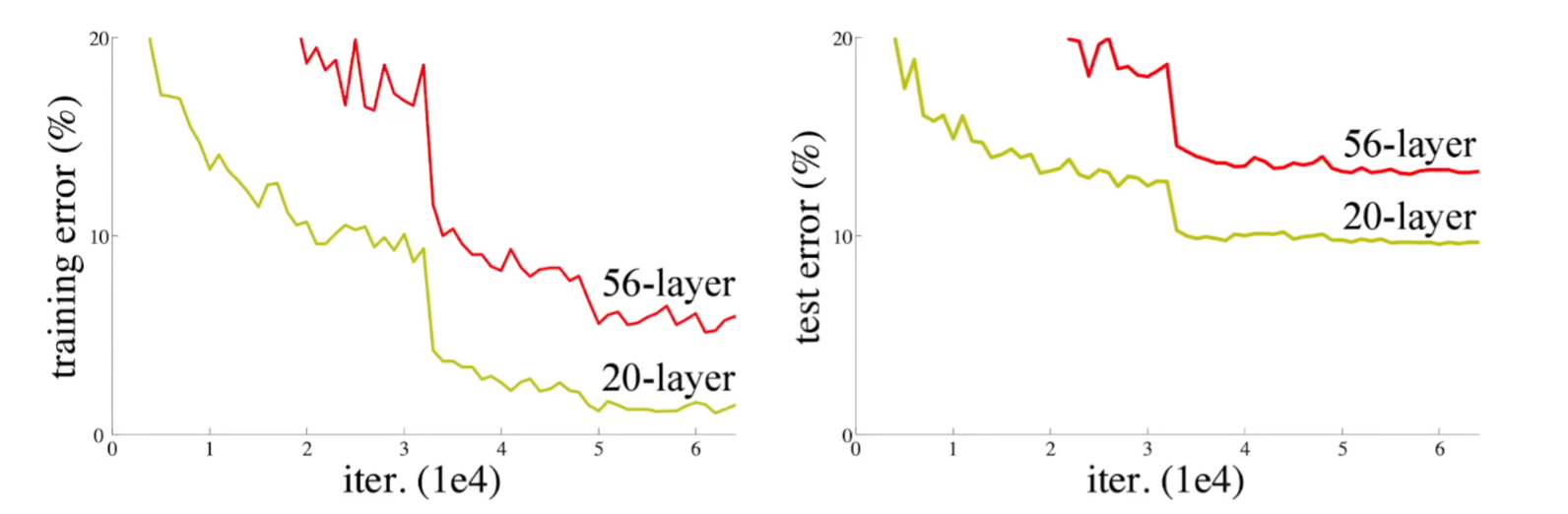
在未使用残差网络的模型中，当网络层数变多时，训练误差以及测试误差均会升高。

Is learning better networks as easy as stacking more layers ?

• 当网络变得特别深时，会出现梯度爆炸或梯度消失
• 传统的解决方法是：参数在初始化时要做的好一点，不要太大也不要太小；加入一些Batch Normalization Layers
• 传统的解决方法使得神经网络能够收敛，但是网络的精度却变得更差，而这并非是模型变得复杂后导致的过拟合问题，因为模型的训练误差也变高了
• 正常来说，如果在一个浅层的神经网络后直接加入更多的层，这些层只做identity mapping，那么这个深层神经网络的误差绝不会高于浅层的神经网络，但是传统的神经网络模型并未找到这样的解（或更好的解）
• 如果深层网络后面的层都是是恒等映射，那么模型就可以转化为一个浅层网络

Deep residual learning framework

• 将残差块的输入与块内最后一个神经网络层的线性输出求和后在进行激活，得到残差块的输出
  
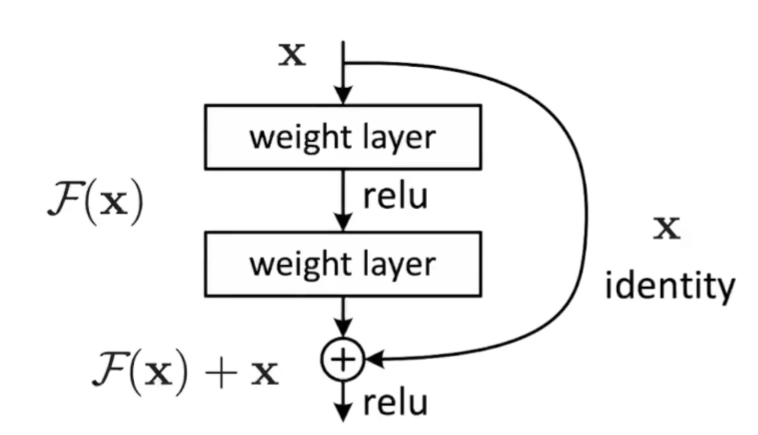
• 残差块只简单地做了shortcut connections，没有引入额外的训练参数，不会增加网络复杂度
• 已有的神经网络很难拟合潜在的恒等映射函数H(x) = x，但是ResNet将残差块设计为H(x) = F(x) + x，其直接把恒等映射作为网络的一部分，只要F(x) = 0，便得到了恒等映射。而此时F(x) = H(x) - x 称为残差函数，就是当前残差块的学习目标（学习出这样一个F(x)函数满足如图输出）
• 值得一提的是，一个残差块中应该至少有两层（中间要包含一个非线性激活），否则就会出现如下情况，这显然是没有用的工作
  

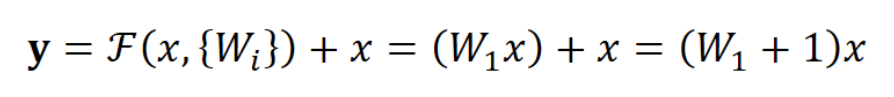
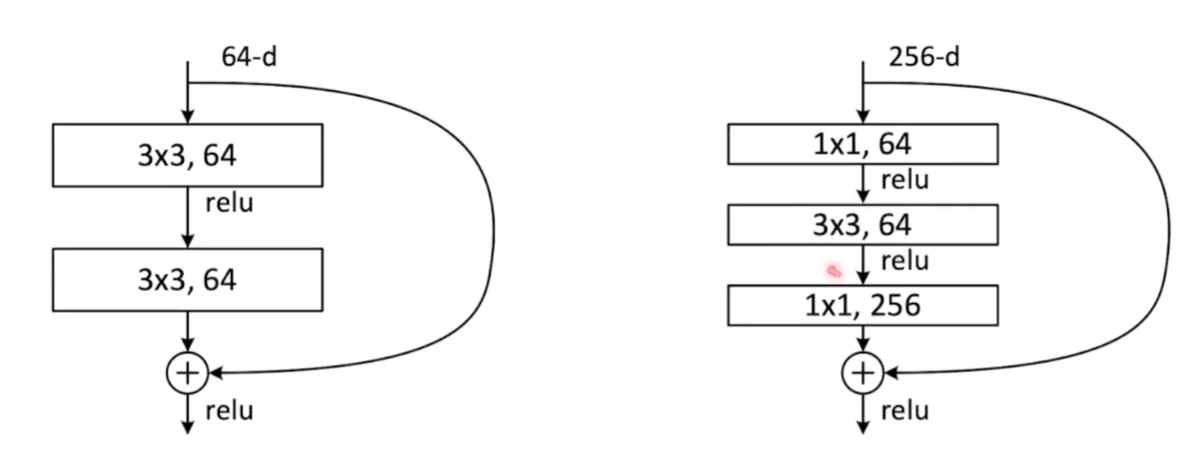
Deeper bottleneck architecture

• 当神经网络层数进一步增多时，参数的增长会带来很大的计算开销。此时可以考虑使用1*1的卷积核暂时减少通道数来减少整个网络的数据规模
  

Analysis of Deep Residual Networks

• 基本BP算法流程如下
  
• 残差块的反向传播过程较好地解释了残差网络避免梯度消失原因，具体推导过程如下
• 推导中忽略偏置项和激活函数