D2L: Matrix
Matrix
Concept and Principle
- 标量
1 | |
- 向量
1 | |
- 矩阵
1 | |
- 运算
1 | |
Derivative
向量上的导数
与向量相关的导数有以下四种形式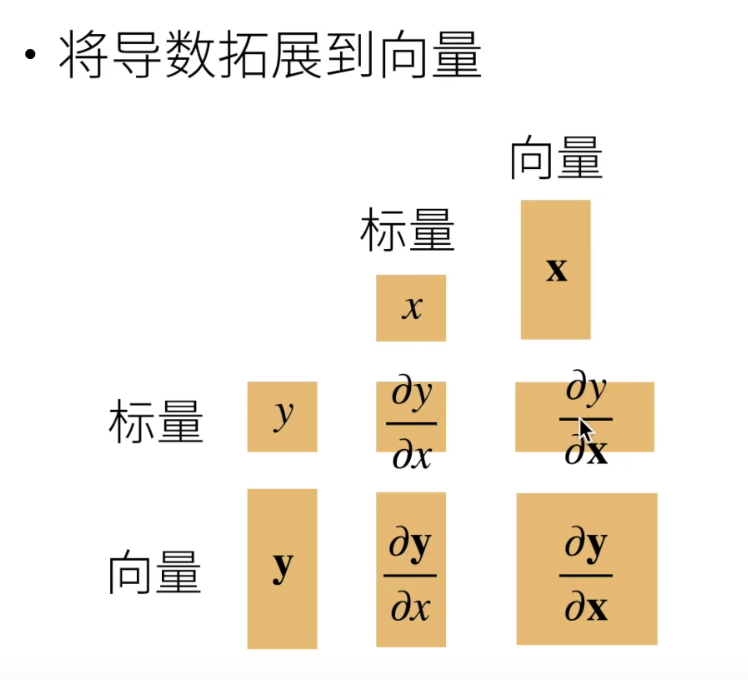
- y标量,x向量
y是由x中各分量计算得到的标量,最终得到y分别每个分量求导得出的向量,这也是梯度的计算过程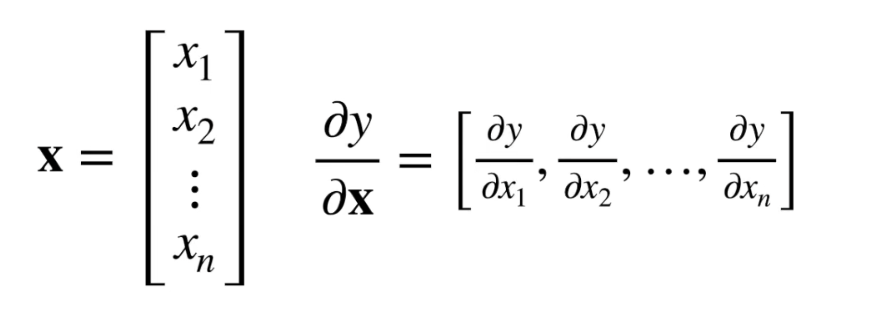
- y向量,x标量
向量y的每个分量都是x的函数,每个分量分别对x求导最终得出一个向量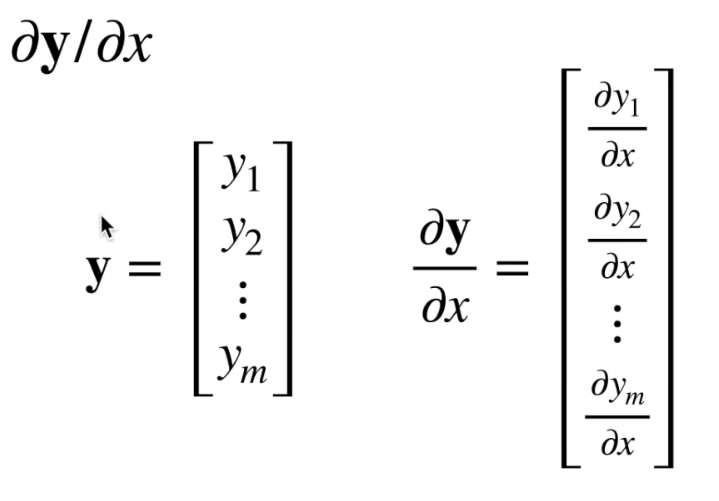
- y向量,x向量
向量y的每个分量都是由x中各分量计算得到的标量,y的每个分量都分别对x的每个分量求导得出一个向量,最后得到一个矩阵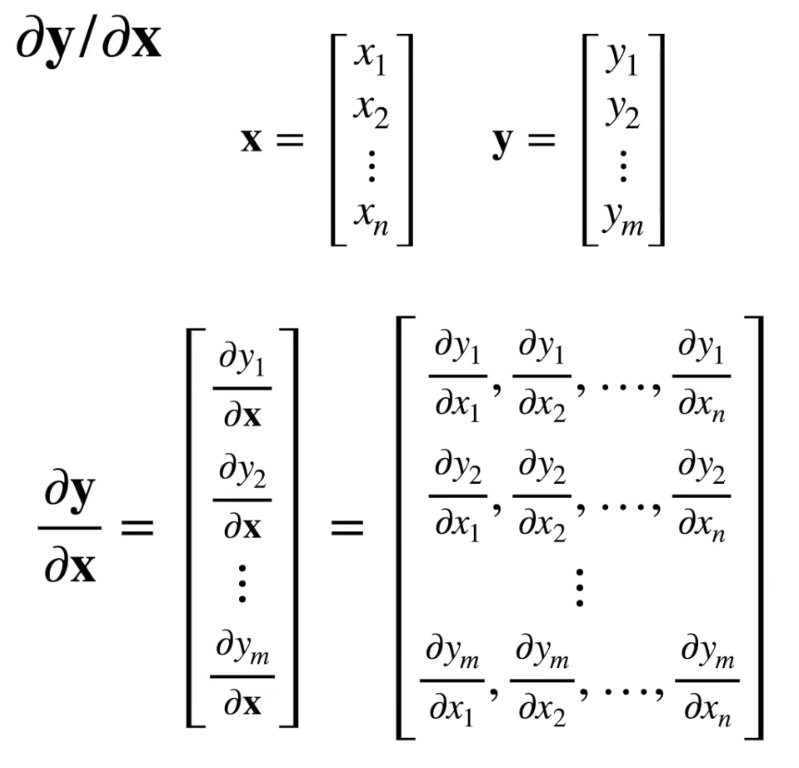
- y标量,x向量
矩阵上的导数
导数同样也可以被扩展到矩阵
Automatic derivative
链式求法则
在神经网络中需要关注向量的链式求导,关键还是要把形状搞对
自动求导
其含义是计算一个函数在指定值上的导数,它不同于符号求导和数值求导- 计算图
计算图本质上就等价于链式求导法则的求导过程,它将计算表示成一个无环图,下面是具体的例子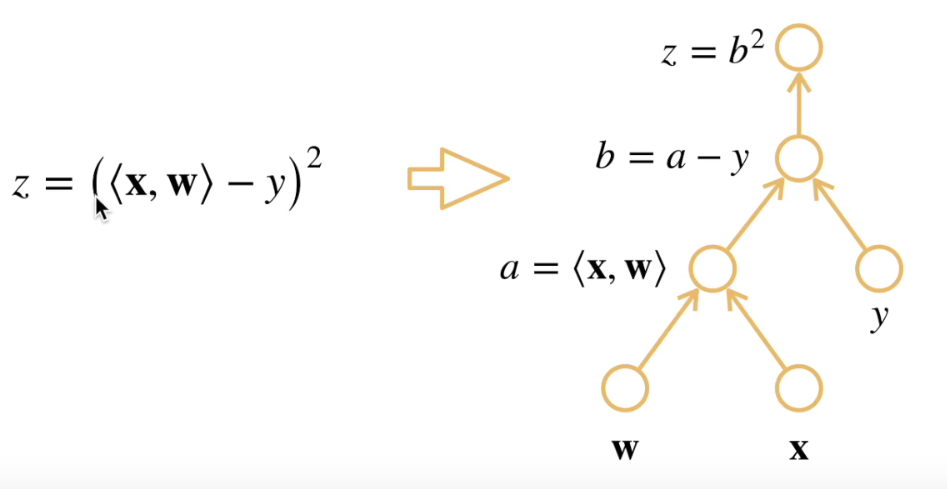
- 反向传播
反向传播解决了自动求导的问题,它利用在前向传播时计算图中存储的计算中间结果,一步一步反向算出链式求导中各步导数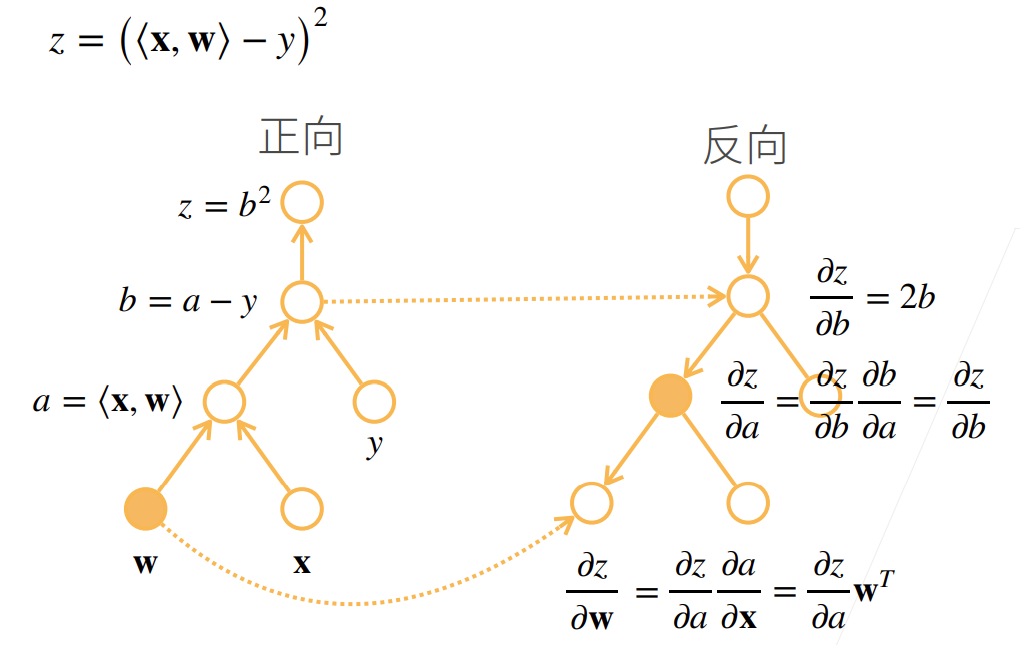
- 自动求导实现
- 计算图
1 | |
Comment