Perceptron

Concept and Principle

  • 感知机
    • 模型
      感知机只比线性分类多了一个激活函数，激活函数为单层感知机带来了分类能力，为多层感知机带来了非线性因素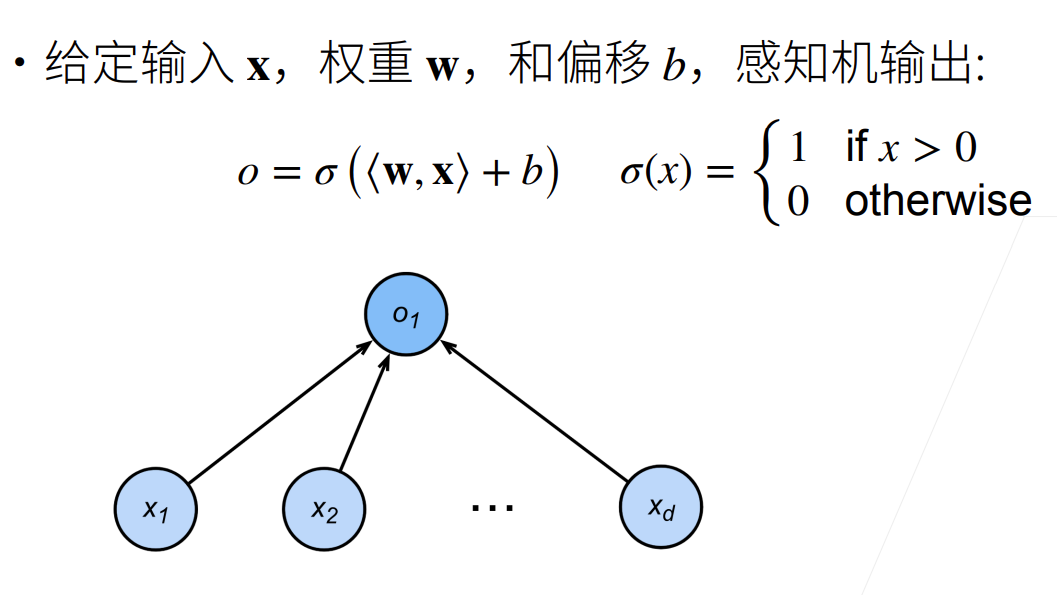
    • 训练
      训练感知机等价于批量大小为1的梯度下降，按顺序逐个取样本，与随机梯度下降不同
    • 单层感知机无法解决异或问题，他只能产生线性分割面，这导致了第一次AI寒冬
  • 多层感知机
    • 多层感知机由多个感知机组成，分为输入层、隐藏层、输出层，层内不连接，层间全连接
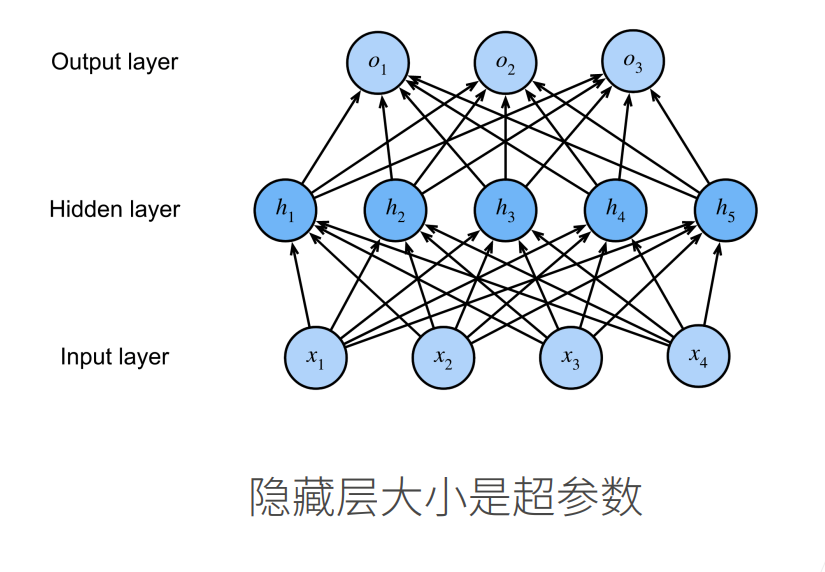
    • 每个感知机输出后要经过一个非线性的激活函数，否则多层感知机等价于单层感知机
    • 常用激活函数：Sigmoiod、Tanh、ReLU，性能都没太大区别，ReLU计算更容易，如果没有特别的想法，用ReLU就行

Implementation

  • 从零实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from torch import nn,optim

train_iter,_=LoadData(256)
num_in,num_out,num_h=784,10,256
# 隐层参数
w1=torch.randn(num_in,num_h,requires_grad=True)
b1=torch.zeros(num_h,requires_grad=True)
# 输出层参数
w2=torch.randn(num_h,num_out,requires_grad=True)
b2=torch.zeros(num_out,requires_grad=True)
params=[w1,b2,w1,b2]

loss_f=nn.CrossEntropyLoss()
opt=optim.SGD(params,lr=0.001)

def ReLU(X):
    a=torch.zeros_like(X)
    return torch.max(X,a)

def Net(X:Tensor):
    X=X.view(-1,num_in)
    # @被重载为了矩阵乘法
    X=ReLU(X@w1+b1)
    return X@w2+b2

def Train():
    for epoch in range(50):
        loss=0
        for X,y in train_iter:
            X=X.view(-1,784)
            out=Net(X)
            l=loss_f(out,y)

            l.backward()
            opt.step()
            opt.zero_grad()
            loss=l.item()
        print(f"{epoch},{loss}")